
Let us just put the value in the integral. Let us just simplify this integration with proper steps:Īs we know about the trigonometric identity i.e. Now, let us just transcribe the integral for the moment of inertia of a circle. Now after the differentiation, the expression will be obtained as

However it would be a reasonable interpretation in this homework problem that thinness means uniform density in this dimension b and that the half circle radius r has a relationship with b of r>100b>0.
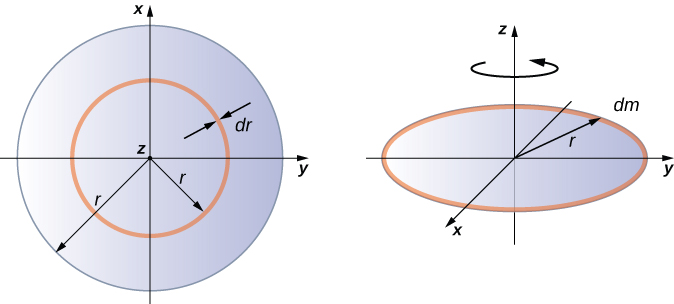
Presently, let us just describe the coordinates by applying the polar system.Īfter the completion of step-1, we need to calculate the differential area, which can be achieved by declaring the area of the sector.įrom the image, the area of the sector can be expressed as Re: Mass Moment of Inertia of a Semi-circle Disk With Mass of M and Radius R. I y is the component of MOI in the y-axis. Let us just begin by remembering the equation for the second-moment area. This explanation will follow certain steps, such as: The moment of inertia formula of a circle, as per the derivation, the circular cross-section will be calculated with the radius and an axis going exactly through the center.
#FIND MASS MOMENT OF INERTIA OF A CIRCLE HOW TO#
It will be easier to understand how to find moment of inertia of a circle with this derivation. This expression for the moment of inertia of a circle about its diameter can be given asĭo you know how to find the moment of inertia of a circle? To learn about this, we need to understand the derivation of the moment of inertia of a circle, as explained below. If we consider the diameter of a circle D, then we must also take ‘r’ the radius as D/2. Moment of Inertia of a Circle about its Diameter In the case of a quarter circle the expression is given as: How do you determine the moment of inertia Calculate the rotational inertia or the moment of inertia by multiplying the mass of the object with square of the distance between the object and the axis, the radius of rotation. In case of a semi-circle the formula is expressed as: momentum of inertia circle: 1.25 : 0.5: 559: 68: Frequently Asked Questions. In the case of a circle, the polar moment of inertia is given as: Similarly, the moment of inertia of a circle about an axis tangent to the perimeter(circumference) is denoted as:
The moment of a circle area or the moment of inertia of a circle is frequently governed by applying the given equation: The moment of Inertia formula can be coined as: Mathematically, it is the sum of the product of the mass of each particle in the body with the square of its length from the axis of rotation. Yes, the proper definition of the moment of inertia is that a body tends to fight the angular acceleration. When a body starts to move in rotational motion about a constant axis, every element in the body travels in a loop with linear velocity, which signifies, every particle travels with angular acceleration. It can be inferred that inertia is related to the mass of a body. That’s one term in the weighted sum of positions, the sum that yields the position of the center of mass.First of all, let us discuss the basic concept of moment of inertia, in simple terms. Now, \(dm\) can be expressed as \(\mu\)\(dx\) so our expression for the term in the weighted sum can be written as The position \(\bar\), so, a term in our weighted sum of positions looks like: Mass Moment of Inertia, I G (cont’d) I G for a body depends on the body’s mass and the location of the mass. Mass Moment of Inertia (Moment of Inertia) - I - is a measure of an objects resistance to change in rotation direction. Thus, for two particles on the \(x\) axis, one of mass \(m_1\), at \(x_1\), and the other of mass \(m_2\), at \(x_2\), To determine the position of the center of mass of the distribution of matter in such a case, we compute a weighted sum of the positions of the particles in the distribution, where the weighting factor for a given particle is that fraction, of the total mass, that the particle’s own mass is. How about if one of the particles is more massive than the other? One would expect the center of mass to be closer to the more massive particle, and again, one would be right. We give the name “center of mass” to the average position of the material making up a distribution, and the center of mass of a pair of same-mass particles is indeed midway between the two particles. Consider two particles, having one and the same mass m, each of which is at a different position on the x axis of a Cartesian coordinate system.Ĭommon sense tells you that the average position of the material making up the two particles is midway between the two particles.


 0 kommentar(er)
0 kommentar(er)
